You're reading the documentation of the v0.6. For the latest released version, please have a look at v0.11.

LOv rewriting rules in Perceval

The aim of this notebook is to rewrite a circuit using rewriting rules based on the article: LOv-Calculus: A Graphical Language for Linear Optical Quantum Circuits.

We show how to use these rewriting rules to generate unique triangular normal forms.

[14]:

import perceval as pcvl
import perceval.lib.phys as phys
from perceval.algorithm.optimize import optimize
from perceval.algorithm.norm import frobenius
import random

This is the first rewrite rule used in this noteobok. It is the rule 37 in the article.

image0

[2]:

pattern1=pcvl.Circuit(3, name="pattern1")//(0,phys.PS(pcvl.P("phi0")))//(0,phys.BS(theta=pcvl.P("theta1")))//(0,phys.PS(pcvl.P("phi2")))//(1,phys.PS(pcvl.P("phi1")))//(1,phys.BS(theta=pcvl.P("theta2")))//(0,phys.BS(theta=pcvl.P("theta3")))
pattern1._color = "lightgreen"
pcvl.pdisplay(pcvl.Circuit(3).add(0,pattern1,False), recursive=True)
0 1 2 Φ=phi0 theta=theta1 Φ=phi2 Φ=phi1 theta=theta2 theta=theta3 PATTERN1 0 1 2
[3]:

rewrite1=pcvl.Circuit(3, name="rewrite")//(0,phys.PS(pcvl.P("beta2")))//(1,phys.PS(pcvl.P("beta1")))//(1,phys.BS(theta=pcvl.P("alpha1")))//(0,phys.BS(theta=pcvl.P("alpha2")))//(1,phys.PS(pcvl.P("beta3")))//(1,phys.BS(theta=pcvl.P("alpha3")))//(0,phys.PS(pcvl.P("beta4")))//(1,phys.PS(pcvl.P("beta5")))//(2,phys.PS(pcvl.P("beta6")))
rewrite1._color = "lightgreen"
pcvl.pdisplay(pcvl.Circuit(3).add(0,rewrite1,False), recursive=True)
0 1 2 Φ=beta2 Φ=beta1 theta=alpha1 theta=alpha2 Φ=beta3 theta=alpha3 Φ=beta4 Φ=beta5 Φ=beta6 REWRITE 0 1 2

Let us implement now the rule number 1.

image0

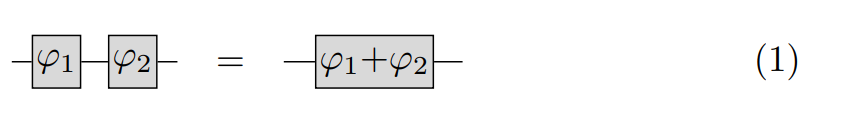
[4]:

pattern2=pcvl.Circuit(1, name="pattern")//phys.PS(pcvl.P("phi1"))//phys.PS(pcvl.P("phi2"))
rewrite2=pcvl.Circuit(1, name="rewrite")//phys.PS(pcvl.P("phi"))

[5]:

pcvl.pdisplay(pcvl.Circuit(1).add(0,pattern2,False), recursive=True)
0 Φ=phi1 Φ=phi2 PATTERN 0
[6]:

pcvl.pdisplay(pcvl.Circuit(1).add(0,rewrite2,False), recursive=True)
0 Φ=phi REWRITE 0

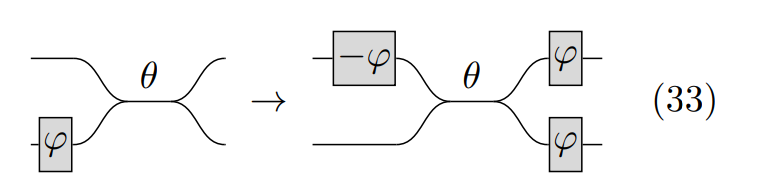
The third rule used in this notebook is the following one:

image0

[7]:

pattern3=pcvl.Circuit(2, name="pattern3")//(1,phys.PS(pcvl.P("phip")))//(0,phys.BS(theta=pcvl.P("theta")))
pattern3._color = "pink"
pcvl.pdisplay(pcvl.Circuit(2).add(0,pattern3,False), recursive=True)
0 1 Φ=phip theta=theta PATTERN3 0 1
[8]:

rewrite3=pcvl.Circuit(2, name="rewrite3")//(0,phys.PS(pcvl.P("phi1")))//(0,phys.BS(theta=pcvl.P("theta")))//(0,phys.PS(pcvl.P("phi2")))//(1,phys.PS(pcvl.P("phi3")))
rewrite3._color = "pink"
pcvl.pdisplay(pcvl.Circuit(2).add(0,rewrite3,False), recursive=True)
0 1 Φ=phi1 theta=theta Φ=phi2 Φ=phi3 REWRITE3 0 1

And the fourth rule is the rule 38 in the article.

image0

[9]:

pattern4=pcvl.Circuit(2, name="pattern4")//(0,phys.BS(theta=pcvl.P("theta1")))//(0,phys.PS(pcvl.P("phi1")))//(0,phys.BS(theta=pcvl.P("theta2")))
pattern4._color = "orange"
pcvl.pdisplay(pcvl.Circuit(2).add(0,pattern4,False), recursive=True)
0 1 theta=theta1 Φ=phi1 theta=theta2 PATTERN4 0 1
[10]:

rewrite4=pcvl.Circuit(2, name="rewrite4")//(0,phys.PS(pcvl.P("beta1")))//(0,phys.BS(theta=pcvl.P("alpha1")))//(0,phys.PS(pcvl.P("beta2")))//(1,phys.PS(pcvl.P("beta3")))
rewrite4._color = "orange"
pcvl.pdisplay(pcvl.Circuit(2).add(0,rewrite4,False), recursive=True)
0 1 Φ=beta1 theta=alpha1 Φ=beta2 Φ=beta3 REWRITE4 0 1
[11]:

a=pcvl.Circuit.generic_interferometer(4, lambda idx:pcvl.Circuit(2)//phys.PS(phi=random.random())//phys.BS(theta=random.random()), depth=8, shape="rectangle")
pcvl.pdisplay(a, recursive=True, render_size=0.7)
0 1 2 3 Φ=0.474571 theta=0.657473 Φ=0.66641 theta=0.1426 Φ=0.01086 theta=0.374754 Φ=0.274048 theta=0.810348 Φ=0.690593 theta=0.601457 Φ=0.55819 theta=0.661321 Φ=0.145303 theta=0.440055 Φ=0.162267 theta=0.905973 Φ=0.058824 theta=0.81882 Φ=0.07461 theta=0.686946 Φ=0.337 theta=0.404614 Φ=0.842403 theta=0.018604 0 1 2 3

Normalizing Circuit

[12]:

import drawSvg as draw
import copy

[13]:

reverse = []
direct=[]
def draw_frame(a):
    if isinstance(a, pcvl.Circuit):
        d = pcvl.pdisplay(a, recursive=True, render_size=0.6)
        reverse.insert(0, d)
        direct.append(d)
        return d
    return a

rules = [(pattern1, rewrite1, "lightgreen"), (pattern2, rewrite2, "lightblue"),
         (pattern3, rewrite3, "pink"), (pattern4, rewrite4, "orange")]

with draw.animate_jupyter(draw_frame, delay=0.1) as anim:
    anim.draw_frame(a)
    while True:
        found = False
        for pattern, rewrite, color in rules:
            start_pos = 0
            while True:
                print("matching pattern", pattern._name)
                matched = a.match(pattern, browse=True, pos=start_pos)
                if matched is None:
                    break
                print("matching ok", matched.v_map)
                idx = a.isolate(list(matched.pos_map.keys()), color=color)
                anim.draw_frame(a)
                for k, v in matched.v_map.items():
                    pattern[k].set_value(v)
                v = pattern.compute_unitary(False)
                print("optimizing rewrite",rewrite._name)
                res = optimize(rewrite, v, frobenius, sign=-1)
                print("found params with distance", res.fun)
                subc = rewrite.copy()
                found = True
                a.replace(idx, subc, merge=False)
                anim.draw_frame(a)
                a.replace(idx, subc, merge=True)
                pattern.reset_parameters()
                rewrite.reset_parameters()
                anim.draw_frame(a)
                start_pos = idx
        if not found:
            break
../_images/notebooks_Rewriting_rules_in_Perceval_22_0.svg
matching pattern pattern
matching pattern pattern3
matching pattern pattern4
matching pattern pattern1
matching pattern pattern
matching pattern pattern3
matching pattern pattern4

This representation is exactly the normal form that we wanted to obtain !

Reference

  1. Clément, N. Heurtel, S. Mansfield, S. Perdrix, B. Valiron. LOv-Calculus: A Graphical Language for Linear Optical Quantum Circuits, arXiv:2204.11787 (2022).